Preview

Гамма коррекция
Яркость источника света измеряют в свечах, или канделах. В физических справочниках есть достаточно полные описания, что считают яркостью света в одну канделу, например, там можно найти точную и довольно бесполезную информацию, что одна международная свеча – это 1,005 новой свечи (канделы).

Важно в данном случае, что в численном измерении яркость, при фиксированном спектре, пропорциональна количеству фотонов.

В компьютере цвета измеряются в пропорциях RGB – красного, зелёного и синего, от 0 до 255. 0 – самый черный цвет, 255 самый белый. Понятно, что яркость одного и того же уровня на различных мониторах и других разнообразных средствах вывода изображений отличается друг от друга. Сказать заранее, какой уровень серого будет соответствовать какой яркости в абсолютных единицах, нельзя.

Тогда попробуем установить, какой уровень серого соответствует излучению в два раза более слабому, чем самый яркий цвет – белый в [255; 255; 255]. Сделать это очень просто – нарисовав вот такую картинку:

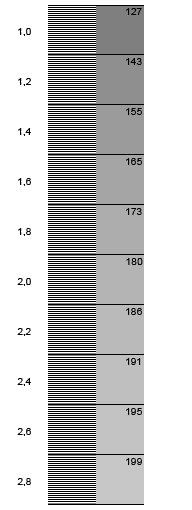
Если прищуриться или просто подальше отойти от монитора, то белые и черные полоски в левом столбце сольются в однотонный фон. Его яркость, понятно, будет как раз в половину мощности самого яркого белого. Можно подобрать, в каком из правых квадратов яркость будет совпадать с левым лучше всего. Самый верхний, с яркостью в 127, что почти совпадает с 255/2, оказывается гораздо темнее, чем яркость половинной мощности. Почему так?

Ответ прост - шкала цветов нелинейная. Следующий резонный вопрос - почему она нелинейная?

Первая причина - так сложилось исторически. Если на вход катода электронно-лучевой трубки подаётся напряжение V, то количество фотонов, или что то же самое, интенсивность света I, которую мы будем наблюдать, будет

I~V^g
Где параметр g - вообще говоря, зависит от трубки.

В реальных условиях формула довольно точно выражает зависимость яркости от "номера цвета". Кроме "чистого", физического эффекта могут применяться различные компенсирующие схемы.

Строго говоря, в данной формуле не учитывается тот факт, что самый черный цвет [0; 0; 0] в реальности соотвествует какому-то слабому излучению. Тут речь идёт о некотором идеальном устройстве вывода, контраст которого бесконечен, а черный - совершенно черён. В жизни, конечно, не так - но для первого приближения неплохо.

Пользуясь верхним рисунком, можно легко определить параметр g, или коэфициент гамма-коррекции для вашего монитора (он написан в левом столбце).

Вторая причина - это оказалось довольно оправданным. Дело в том, что гамма-компенсированная шкала, по сравнению с линейной, точнее передаёт тёмные цвета, близкие к черному. Чувствительность человеческого зрения также нелинейна, мы хорошо чувствуем относительные изменения яркости, а не абсолютные.

Когда микросхемы были большими, а программы маленькими, выделять больше одного байта на компоненту R, G и B казалось ненужным и расточительным. Если бы шкала была 8-битной и линейной, то градиент выглядел бы примерно так:

Вот иллюстрация разницы между 8-битными (256 уровней серого) линейной и гамма-компенсированной шкалой. Темные цвета вторая шкала передаёт значительно точнее. В линейной шкале (на 256 уровней серого) для промежуточных тёмных цветов просто нет места.

Часто возникает вопрос - но ведь при гамма-компенсации теряется точность передачи светлых оттенков! С математической точки зрения - верно. Но с точки зрения человеческого зрения - не совсем. Как уже было сказано, человек чувствует относительные изменения яркости, а не абсолютные. Если в комнате включить третью лампочку на 60 ватт - разница будет заметна хорошо. Если тридцатую - практически неощутима.

Поскольку хранятся и обрабатываются цвета в шкале с гамма-компенсацией, то от всех устройств получения изображений (сканеров и цифровых фотоаппаратов) также требуется перевод в гамма-компенсированную шкалу. Скажем, для цветового пространства sRGB и AdobeRGB этот параметр составляет 2,2. Эта же величина является стандартом для среды Windows. В MacOS принят стандарт 1,8.

На самом деле в sRGB используется более сложная система (wikipedia:sRGB) - смесь линейной и гамма-компенсированой с показателем 2,4. В первом приближении она как раз похожа на просто гамма-шкалу, с коэфициентом в 2,2. Что же до Adobe RGB, то вот что: точный показатель гамма составляет не 2,2 а 2,19921875. Кому может понадобится такая точность?

Как результат, например в LCD мониторах, проекторах и так далее используется также гамма-компенсированная шкала, хотя зависимость между входным напряжением и яркостью там гораздо сложнее. Для достижения этого эффекта используются компенсирующие схемы.

Зачем это знать?

Если бы программисты графических редакторов писали их таким образом, что эффект гамма коррекции учитывался при применении фильтров, то знать было бы не нужно. Однако до самого последнего времени никто не заморачивался.

Возможность обработки изображения в линейной шкале была введена только в photoshop версии CS2. В этом режиме цвет хранится как число с плавающей запятой, что обеспечивает очень большую точность (32 битный float), а также возможность хранить цвета "светлее белого". Такие фильтры, как коррекция экспозиции (цифровой push/pull), корректировка баланса белого в линейной шкале записываются просто умножением компоненты на число. Для гамма-компенсированой нужна последовательность - перевод в линейную, обработка, перевод обратно.

Пример первый. Задача: уменьшить картинку stripes.jpg (~ 100 Kb) с размера 500 на 500 пикселей до размера 200 на 200 пикселей. Результаты:

Результат слева был получен стандартным способом, линейной интерполяцией 8 бит на канал. Картинка справа - в режиме 32 бита на канал, при этом точно также использовалась линейная интерполяция. Сравните муар на правой и левой картинке.

Пример второй. Предположим нам надо размыть картинку, максимально похоже на то, как это делает объектив.